Matrix Modifiers
Matrix Blend
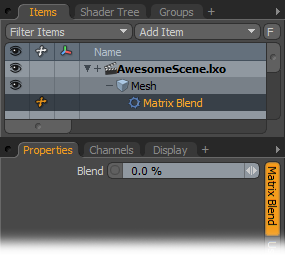
You can use this Channel Modifier to blend between a pair of Rotation or Translation input matrices.
Matrix A/Matrix B: Specify the two matrices to be blended into these channels. These can be World or Local transform matrices from 3D items or the matrix output from other Channel Modifier items. For the best results, link channels with matrices of the same type.
Blend: Modo uses this blend amount to apply to the input matrices. With a value of 0%, Modo outputs the Matrix A matrix unaltered; with 100% Modo outputs the Matrix B matrix unaltered. For values between 0% and 100%, Modo interpolates the matrices between the two inputs. For Rotation matrices, Modo uses a quaternion interpolation, and for Translation matrices, Modo uses a linear interpolation.
Matrix Output: Modo passes the result of the interpolation to this channel. You can link this to a compatible matrix channel on a 3D item or another Channel Modifier.
Matrix Compose
The Matrix Compose Channel Modifier multiplies two or more input matrices together and passes the resulting transform matrix.
Matrix Inputs: This channel accepts multiple input links from the matrix channels of 3D items or other Channel Modifier outputs. Modo multiples the matrices together in the order that you used when you linked them this channel.
Matrix Output: Modo outputs the composed matrix to this channel. You can link this into a compatible matrix channel on a 3D item or another Channel Modifier's input.
Matrix Construct
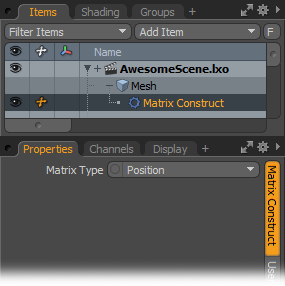
The Matrix Construct modifier creates a 4x4 Transformation matrix from a vector.
Input X/Input Y/Input Z: Describes either the position or the scale of the resulting matrix.
Matrix Type: Specifies whether the output is a Position matrix or a Scale matrix.
Output: Modo passes the composed matrix to this channel.
Matrix From Euler
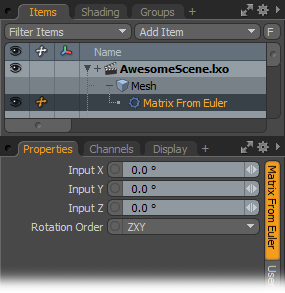
The Matrix From Euler modifier extracts a vector that represents rotation angles in the X, Y and Z axes from a 4x4 Rotation matrix.
Input X/Input Y/Input Z: Describes rotation angles around the X, Y, and Z axes.
Rotation order: Describes the rotation order of the three axes. With the default ZXY order, Modo calculates the final matrix by creating a matrix to represent the Z axis, then creating a matrix to represent the X axis, and finally creating a matrix to represent the Y axis. Modo then multiples the three matrices together to construct the final matrix.
Output: Outputs the resulting rotation matrix.
Matrix To Euler
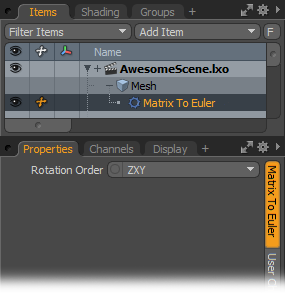
The Matrix To Euler modifier extracts a vector that represents rotation angles in the X, Y, and Z axes from a 4x4 Rotation matrix.
Input X/Input Y/Input Z: Indicates the input rotation matrix from which to extract rotation angles.
Rotation Order: Describes the rotation order of the three axes. With the default ZXY order, Modo calculates the final matrix by creating a matrix to represent the Z axis, then creating a matrix to represent the X axis, and finally creating a matrix to represent the Y axis. Modo then uses the three matrices to construct the final matrix.
Output X/Output Y/Output Z: Describes rotation angles around the X, Y, and Z axes.
Matrix Invert
The Matrix Invert modifier inverts the transforms stored in the input matrix. For example, if the input matrix stores rotations of 90, 45, and 180 degrees, the output matrix stores the opposite: -90, -45, and -180 degrees. It also outputs the inverse of position and scale, or a combination of all three.
This modifier can be extremely useful, as often it's desirable to perform complex 3D math operations at the center of the world. Multiplying a transform matrix by it's inverse transform matrix, results in an identity matrix. That is to say, a matrix that stores no position, rotation, and 100% scale. This allows you to easily transform an item back to its center position, perform a maths operation easily, and then transform it back by multiplying by the original transform.
Input: The matrix to invert.
Output: The resulting inverse matrix.
Matrix Transpose
The Matrix Transpose modifier inverts a 4x4 matrix across the main diagonal. Modo inverts any rotation stored in the matrix; therefore, for example, a rotation of 90 degrees in X becomes a rotation of -90 degrees.
Input: Indicates the matrix with the values to transpose.
Output: Indicates where Modo should pass the matrix with the transposed values.
Matrix Vector
You use this Channel Modifier to extract a normalized direction vector from a Rotation matrix or the translation row from a Translation matrix. Direction vectors in a Rotation matrix are the axes formed after the individual X, Y, and Z rotations have been performed. For example, given the World Rotation matrix of a 3D item, the Z Direction vector points in the direction the item is facing, and the Y axis points towards the top of the item.
Matrix Input: Links the matrix channel from which the vector is to be extracted into this channel. This can be a matrix channel from a 3D item or the output matrix from another Channel Modifier.
Row: This specifies whether to extract the X, Y, Z direction vector from a Rotation matrix or the translation from a Translation matrix.
Output X/Output Y/Output Z: Passes the vector extracted from the matrix to these three channels.
Matrix Vector Multiply
The Matrix Vector Multiply modifier multiplies a transform matrix by a vector, and outputs the resulting vector. This essentially applies any transforms that are stored in the matrix to the vector. For example, if the vector stored a value of [1.0, 0.0, 0.0] and the matrix stored a position of 2m in X, then the resulting vector would be [3.0, 0.0, 0.0].
This modifier is really useful when used with rotation matrices. For example, if you have a ray that is fired from a point in space, by multiplying the ray vector by the rotation matrix, you can easily change the direction of the ray, rotating it by whatever value is stored in the matrix.
Matrix: The matrix to multiply the vector by.
Input: The vector to multiply by the matrix.
Output: The resulting vector.