Vector Modifiers
Vector
A vector is a position with both direction and intensity. You can use Vector modifiers when creating vectors, setting their length, and normalizing them (setting their length to 1).
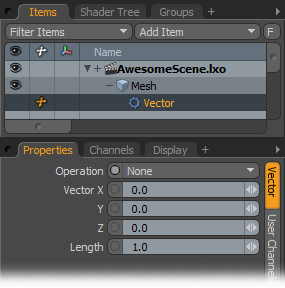
Operation: The available vector operations are:
• None - Creates a vector to link to other Channel Modifiers or Item channels.
• Normalize - Sets the length of the Input vector to 1.0.
• Set Length - Sets the length of the Input vector to the value set in the Length channel.
Vector X/Y/Z: Specifies the X, Y, and Z coordinates of the Input vector.
Length: Specifies the length of the vector for the Length operation.
Vector Magnitude
This modifier measures the length (or magnitude) of a vector. There are no specific options for this modifier.
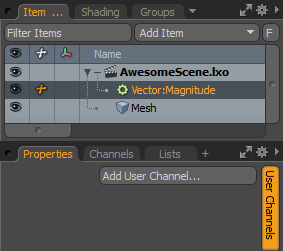
Start: Specifies the vector to be measured.
End: Defines the end points of the vector. This is optional, but available in case the vector's origin is not 0,0,0.
Magnitude: Indicates the length of the vector.
Vector Maths
Provides some basic mathematical operations for Modo to perform on 2 Input vectors.
Note: In the case of the dot product, which is a single floating point value, Modo writes the result to the first output channel only (Output X).
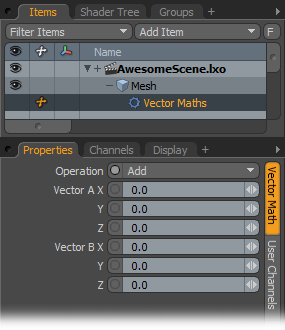
Operation: Specifies the math operation to apply:
• Add - Adds the two Input vectors.
• Cross Product - Determines a vector that is at right angles to the two Input vectors on the plane containing them.
• Dot Product - Determines the cosine of the angle between the two Input vectors.
• Subtract - Subtracts the Input vectors.
Vector A X/Y/Z: Indicates the X, Y, and Z coordinates for vector A.
Vector B X/Y/Z: Indicates the X, Y, and Z coordinates for vector B.
Vector Orthogonalize
The Vector Orthogonalize modifier orthogonalizes vectors so that no components on the input vector match a second normal vector.
For example, if the input vector is [0.5, 0.5, 0.0] and the normal vector is [1.0, 0.0, 0.0], then the output vector should be [0.0, 0.5, 0.0], as the modifier removes any values aligned to normal - in this case is the entire X component. This also works on non-axis aligned vectors.
The resulting output vector is at a right angle to the normal vector, unless the input vector and normal are aligned, in which case the output vector has a length of zero.
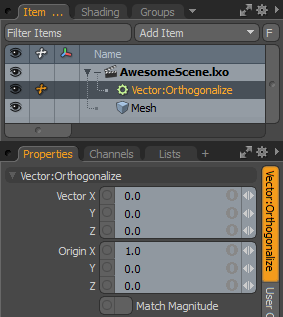
Vector: Specifies the vector to be orthogonalized.
Normal: Specifies the vector that no components of the input vector match.
Match Magnitude: When enabled, match the magnitude of the output vector with the input vector. For example, if the input vector is [0.7071, 0.7071, 0.0], it has a length or magnitude of 1.0. If the normal vector is [1.0, 0.0, 0.0], this results in an output vector of [0.0, 0.7071, 0.0], which means that the magnitude or length of the vector has become 0.7071. The Match Magnitude channel sets the output vector back to the correct length, resulting in an output vector of [1.0, 0.0, 0.0].
Output: Outputs the orthogonalized vector.
Vector Reflection
The Vector Reflection modifier is used for calculating a reflection across a position and normal.
In simple terms, if you have a surface at a position defined by the Origin channel, and its normal is defined by the Normal channel, then a position defined by the Vector input is reflected to a position that matches the Output channel.
Vector: Specifies the input position to be reflected.
Origin: Specifies the origin of the reflection. For the majority of cases, leaving this at [0.0, 0.0, 0.0] should be sufficient.
Normal: Specifies the Normal of the surface that the input vector is being reflected in. Essentially, this is defining the axis that is used for reflection.
Output: Outputs the reflected position of the input vector.
Vector Multiply by Scalar
The Vector Multiply by Scalar modifier takes a vector and multiplies each component by a single scalar input. For example, if the vector is [1.0, 0.5, 0.25] and the scalar is 2.0, then the output vector is [2.0, 1.0, 0.5].
Tip: The Vector Multiply by Scalar modifier can be used instead of individual Math nodes to perform the same function.
Vector: Specifies the vector to be multiplied.
Amount: Specifies the scalar amount to multiply the vector by.
Output: Outputs the multiplied vector.