The Quaternion Conjugate modifier calculates the inverse of a quaternion. For example, if the input quaternion contains a rotation of 45 degrees in Y, the output quaternion contains a rotation of -45 degrees in Y.

Input: The quaternion to conjugate.
Output: Outputs the conjugated quaternion.
The Quaternion From Axis-Angle modifier converts a rotation around an arbitrary axis into a quaternion.
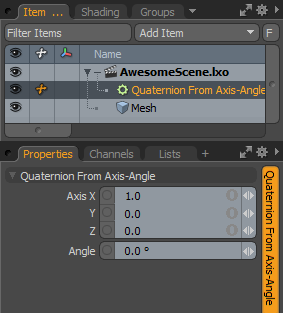
Axis: The axis to perform the rotation around.
Angle: The rotation angle to rotate around the axis.
Quaternion: Outputs the result.
The Quaternion From Euler modifier converts XYZ rotation angles into a quaternion.
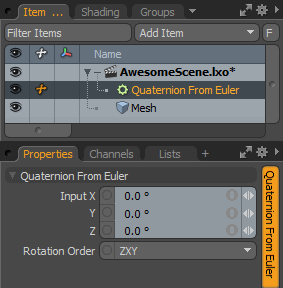
Input: The XYZ rotation angles to convert.
Rotation Order: The order used for combining the three axes. As euler rotations use three gimbals, the order of the rotation matters. For example, if the Rotation Order channel is set to ZXY (default), the Z rotation is performed first, without affecting the other axes. Next, the X axis rotates, changing the plane used to define the Z axis. Finally, the Y axis is calculated, which changes the plane used to define both the X and Z. In the majority of cases, this value should match the value in the Modo transform properties.
Quaternion: Outputs the result.
The Quaternion From Matrix modifier converts a rotation matrix into a quaternion.
Matrix: The rotation Matrix to convert.
Quaternion: Outputs the result.
The Quaternion Get Value modifier returns the four components representing the value of the quaternion.
Input: The input quaternion to read for its values.
Value: The first three components stored in the quaternion.
Value W: The fourth component stored in the quaternion.
The Quaternion Math modifier performs simply math operations on two quaternions: Add, Subtract, Multiply, or Divide. In some operations, the quaternion inputs are non-commutative, so swapping Quaternion A and Quaternion B around, changes the result. These modifiers show up as four separate modifiers in the interface, but they are in fact a single modifier that has multiple math operations.
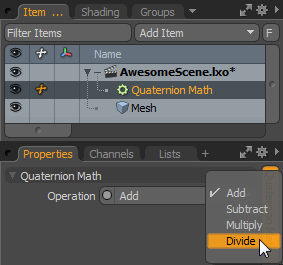
Quaternion A: The first quaternion used for the math operation.
Quaternion B: The second quaternion used for the math operation.
Operation: The math operation to perform: Add, Subtract, Multiply, or Divide.
Output: The resulting quaternion, after the math operation has been performed.
The Quaternion Normalize modifier normalizes a quaternion, so that it has a magnitude of 1.0.
Input: The quaternion to normalize.
Output: The normalized quaternion.
The Quaternion Set Value modifier sets the four components representing the value of the quaternion.
Value: The values used to set the first three components stored in the quaternion.
Value W: The value used to set the fourth component stored in the quaternion.
Output: The resulting quaternion.
The Quaternion Slerp modifier performs a Spherical Linear Interpolation between two quaternions, blending the rotation stored in one quaternion to the rotation stored in another quaternion.
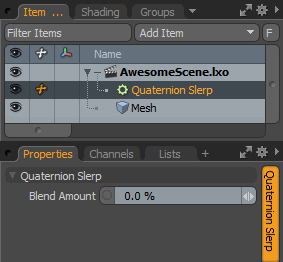
Quaternion A: The first quaternion value to blend from.
Quaternion B: The second quaternion value to blend to.
Blend Amount: The amount of blend between the two quaternions. A value of 0 returns Quaternion A and a value of 100 returns Quaternion B. A value in between these two values returns an interpolation between the two quaternions.
Output: The resulting quaternion.
The Quaternion To Axis-Angle modifier converts a quaternion into a rotation around an arbitrary axis.
Quaternion: The quaternion to convert to an axis-angle.
Axis: The axis the rotation is performed around.
Angle: The rotation angle performed around the axis.
The Quaternion To Euler modifier converts a quaternion into XYZ rotation angles.
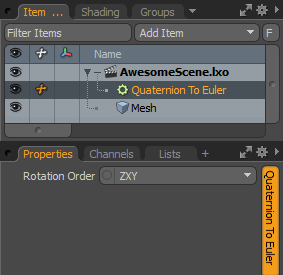
Quaternion: The quaternion to convert into XYZ rotation angles.
Rotation Order: The order used for combining the three axes. As euler rotations use three gimbals, the order of the rotation matters. For example, if the Rotation Order channel is set to ZXY (default), the Z rotation is performed first, without affecting the other axes. Next, the X axis rotates, changing the plane used to define the Z axis. Finally, the Y axis is calculated, which changes the plane used to define both the X and Z. In the majority of cases, this value should match the value in the Modo transform properties.
Output: The resulting XYZ rotation angles, converted from the quaternion.
The Quaternion To Matrix modifier a quaternion into a rotation matrix.
Quaternion: The quaternion to convert into a matrix.
Matrix: Outputs the resulting rotation matrix.
The Quaternion Vector Multiply modifier, multiplies a vector by a quaternion. This essentially rotates the vector around the axis stored in the quaternion, by the angle stored in the quaternion.
Quaternion: The quaternion to multiply the vector by.
Input: The input vector to multiply by the quaternion.
Output: The resulting vector.