四元数修饰符
四元数共轭
的Quaternion Conjugate修饰符可计算四元数的逆数。例如,如果输入四元数包含Y的45度旋转,则输出四元数包含Y的-45度旋转。
Input:四元数共轭。
Output:输出共轭四元数。
四元数从轴角
的Quaternion From Axis-Angle修饰符可将围绕任意轴的旋转转换为四元数。
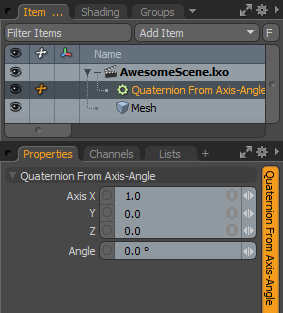
Axis:执行旋转的轴。
Angle:绕轴旋转的旋转角度。
Quaternion:输出结果。
欧拉四元数
的Quaternion From Euler修改器可将XYZ旋转角度转换为四元数。
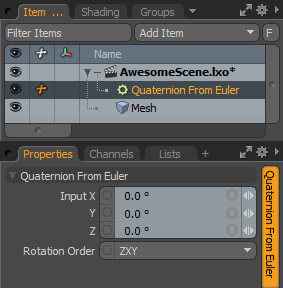
Input:要转换的XYZ旋转角度。
Rotation Order:用于组合三个轴的顺序。由于欧拉旋转使用三个云台,所以旋转的顺序很重要。例如,如果Rotation Order频道设置为ZXY (默认), Z首先执行旋转,而不影响其他轴。接下来, X轴旋转,更改用于定义Z轴。最后, Y计算轴,这将更改用于定义两个X和Z。在大多数情况下,该值应与Modo转换属性。
Quaternion:输出结果。
矩阵四元数
的Quaternion From Matrix修饰符可将旋转矩阵转换为四元数。
Matrix:要转换的旋转矩阵。
Quaternion:输出结果。
四元数获得价值
的Quaternion Get Value修饰符返回代表四元数值的四个分量。
Input:输入四元数以读取其值。
Value:前三个分量存储在四元数中。
Value W:第四分量存储在四元数中。
四元数数学
的Quaternion Math修饰符仅对两个四元数执行数学运算: Add, Subtract, Multiply, or Divide。在某些操作中,四元数输入是不可交换的,因此交换Quaternion A和Quaternion B周围,更改结果。这些修饰符在界面中显示为四个单独的修饰符,但实际上它们是具有多个数学运算的单个修饰符。
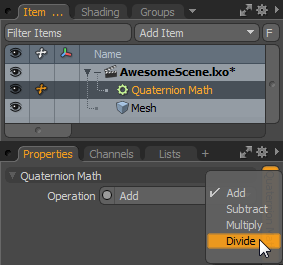
Quaternion A:用于数学运算的第一个四元数。
Quaternion B:第二四元数用于数学运算。
Operation:要执行的数学运算: Add, Subtract , Multiply , 要么Divide。
Output:在执行数学运算之后,生成的四元数。
四元数归一化
的Quaternion Normalize修饰符可将四元数归一化,因此其大小为1.0。
Input:将四元数归一化。
Output:标准化四元数。
四元数设定值
的Quaternion Set Value修饰符设置代表四元数值的四个分量。
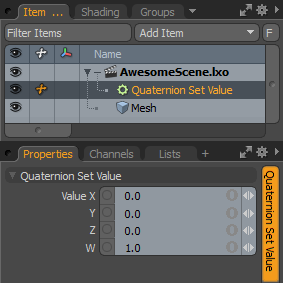
Value:该值用于设置存储在四元数中的前三个分量。
Value W:该值用于设置存储在四元数中的第四个分量。
Output:产生的四元数。
四元数勒
的Quaternion Slerp修饰符在两个四元数之间执行球面线性插值,将一个四元数中存储的旋转与另一个四元数中存储的旋转混合。
Quaternion A:要混合的第一个四元数值。
Quaternion B:要混合的第二个四元数值。
Blend Amount:两个四元数之间的混合量。值0将返回四元数A,值100将返回四元数B。这两个值之间的值将返回两个四元数之间的插值。
Output:产生的四元数。
四元数到轴角
的Quaternion To Axis-Angle修饰符可将四元数转换为围绕任意轴的旋转。
Quaternion:将四元数转换为轴角。
Axis:围绕其旋转的轴。
Angle:绕轴旋转的角度。
四元数到欧拉
的Quaternion To Euler修改器可将四元数转换为XYZ旋转角度。
Quaternion:将四元数转换为XYZ旋转角度。
Rotation Order:用于组合三个轴的顺序。由于欧拉旋转使用三个云台,所以旋转的顺序很重要。例如,如果Rotation Order频道设置为ZXY (默认), Z首先执行旋转,而不影响其他轴。接下来, X轴旋转,更改用于定义Z轴。最后, Y计算轴,这将更改用于定义两个X和Z。在大多数情况下,该值应与Modo转换属性。
Output:从四元数转换得到的XYZ旋转角度。
四元数到矩阵
的Quaternion To Matrix将四元数修改为旋转矩阵。
Quaternion:将四元数转换为矩阵。
Matrix:输出结果旋转矩阵。
四元数矢量乘
的Quaternion Vector Multiply修饰符,将向量乘以四元数。这实质上使矢量围绕四元数中存储的轴旋转四元数中存储的角度。
Quaternion:将向量乘以的四元数。
Input:要乘以四元数的输入向量。
Output:所得向量。